很多人都是从数字开始逐渐积累起对于数学这门学科巨大的兴趣的，如果你格外再有毅力一些，有天赋一些，甚至更幸运一些，是有可能走上数学家的道路的。以数学为终身奋斗的目标，尽情地在数学的海洋里游历。

数海遨游

从1,2,3...开启了我们的数学旅途。很快我们发现了各种各样的数字，有素数，完全数，相亲数，立方数，三角数等等，无穷无尽。如果对数学发展再了解多一点，你就会发现，在这些有一种非常顽固的数字，说它顽固，是因为人们研究它们几千年，却仍然知之甚少。它们就静静地躺在自然数的海洋里，你发现它，它就在，你没有找到它，它就一直沉匿着。

一般情况下，我们研究一些数字，那就会想方设法找到它们的规律，比如它在某种计算情况下会出现，或者它有些奇妙的性质，可以在某些生活场合中体现出来。比如斐波那契数列，递推关系如此简单，但是这个数列中蕴含的奥秘，一千多年来从未停止发现。以至于有专门的机构出版了《斐波那契季刊》，时时更新关于这个数列的最新研究，五十多年多去了也从未停刊。

素数——数学界永久的谜

研究某一种数，最最直接的方法就是找出这种数的公式表示方法，有了通项公式，一切的研究就显得水到渠成。研究一个公式，总比在汪洋数海里摸索容易得多吧。鉴于人们曾经给很多特殊的数字成功地找到了所谓的通项公式，于是在心底里也做起了这样的美梦，素数到底有没有通项公式呢？

拉格朗日

用一个公式就可以表示所有的素数，这在数学界看来不亚于，人类可以像坐地铁一样来回穿梭月球。事实上，两千年来，人们绞尽脑汁，无数人耗尽一生心血，都没有做到，甚至连靠近的机会都没有。如果你对数学的历史了解更多一点，你会发现有无数的数学大牛们，阿基米德，毕达哥拉斯，欧拉，高斯，黎曼，费马，莱布尼茨，勒让德。。。都曾为了这个梦想努力过，然而都没有结果了。我们在感叹这些前辈们的聪明智慧和无比的毅力以外，不经感叹，素数的秘密就这么难揭开吗？

费马

这里，有人曾经脑洞大开：会不会有这样一种情况，人们穷尽两千年都没有找到的素数公式，其实有一种很简单的表示方法，只不过它非常非常幸运地躲过了两千年来所有人的围追堵截，一直隐藏到今天。

其实晓然菌也希望素数公式其实没有那么难，也许真的就有一种非常简单的表示方式。但是稍加思考，顿时心灰意冷。这种情况绝无可能！

咖啡渍也像是一条鱼的巧合

你可以在很多场合下遇到非常巧合的事件发生，比如今天你在外地出差，然后在外地碰到了大学同学，的确很巧合。你今年填报志愿，已经不抱希望的情况下，填了某所大学的竞争非常大的专业，而你并没有多少优势，最后仍然顺利录取，的确也很巧合。然而，数学研究上的所谓巧合，其实都不是巧合，很多看似显然的巧合，背后都是呕心沥血的结果。这里说一个数学研究历史上的漏网之鱼。这个成果被前面很多数学大神们错过，却被一个16岁的青年发现。

220,284这对数字看似平淡无奇，其实是很有意思的。220的所有真约数之和1+2+4+5+10+11+20+22+44+55+110=284，而284的所有真约数之和1+2+4+71+142=220。这么一看220,284就像是你中有我，我中有你，所以人们给这样的数对起名相亲数，实在太形象不过了。这么有趣的现象，人们当然会想尽办法找到更多的例子来。1636年，费马发现了第二对相亲数，17296和18416。1638年，笛卡尔也发现了一对，9363584和9437056。笛卡尔发现的这对相亲数已经不算小了，再到后面恐怕难度越来越大。

无处不在的欧拉

很快相亲数的概念被欧拉知道了，欧拉这个老流氓岂肯错过。1750年，欧拉居然一口气发布了60对相亲数！你没看错，就是一下子发布了60对！人们惊呼欧拉快要把相亲数找完了。再到后面，寻找难度就越来越大了，在当时只能手算的情况下，找寻的兴趣就已经不算大了。然而，在找寻相亲数这个过程里发生了峰回路转的一件事。

1866年，16岁的意大利青年巴格尼尼也发现了一对相亲数，倒不是这对数字是多么多么地庞大，恰恰相反，他找到的这对相亲数仅仅比220,284大一点点，1184,1210。可以想象，如果在在他之前的大神们知道了这对数字，会不会搬起石头砸自己的脚，眼皮底下的这对数字无一例外被错过了。这也是数学史上为数不多但是很精彩的一次漏网之鱼。而那位青年巴格尼尼也因为找到了这对第二小的相亲数，在数学史上永远留下了名字。

大家别太有期待，上面漏网之鱼的案例实在是太少了，几乎没有可重复性。从正面跟素数这个超级硬骨头杠实在是太没有说服力，我们不妨从素数的几个周边问题来说明一下这个问题的难度。

首先我们来探讨探讨素数个数的问题。

高斯

其实很早以前就有人研究过这个问题，但是都不算是很系统的成果，直到少年高斯在15岁那年的惊为天人的类比，让人们第一次摸到了素数个数这个领域的门槛。少年高斯曾经有着一本对数书，书本后面的附件里有一张大约有几千个素数的表格。正常人不会对这样的素数表产生任何兴趣，仅仅会把这个当成工具书，需要的时候拿出来翻翻。然而高斯岂是常人，他也无聊中翻着翻着，突然就觉得这里会有一些奥秘。我能不能从这几千个素数的分布中找到素数个数的公式呢？

于是他开始类比，并做了下面这个表。

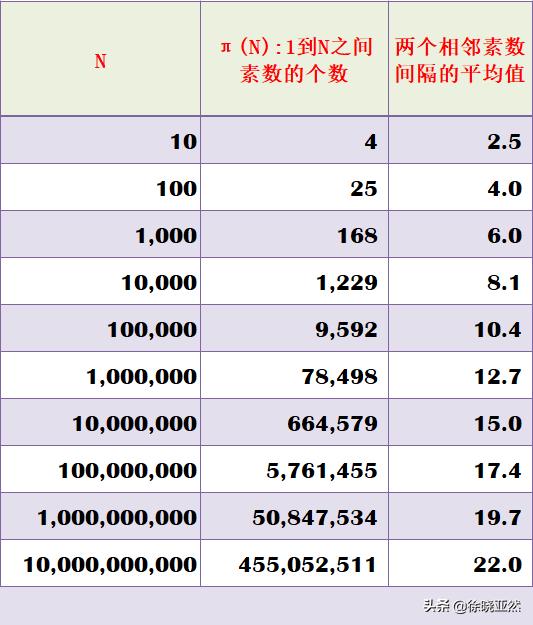
相邻素数间隔平均值统计

高斯敏锐地发现，最右边的那个相邻素数间隔的平均值并没有随着N的10倍增长而同步倍增，看起来好像是左侧增加十倍，右侧始终增加2.3左右。这个不就是对数函数才有的性质嘛，于是，高斯大胆猜测了素数个数的性质。

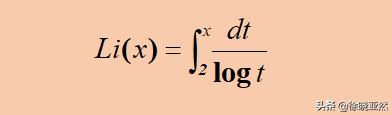
素数定理

当然这是高斯猜测的结果，并没有在理论上进行严格证明。直到20世纪初，高斯的猜测才被证明是正确的。即使没有证明，但是能够提出来这样的猜想也绝非等闲之辈。

如果说高斯的素数定理只是关于素数个数的入门级的研究，那黎曼这位超级大神的黎曼猜想那绝对是素数个数问题终极答案了。

黎曼

1859年，黎曼为了感谢自己当选柏林科学院的通信院士，向科学院发布了一篇仅有8页但内容旷古绝今的论文《论小于给定数值的素数个数》。这篇文章通过对于一个特殊复函数的非平凡零点来研究整个素数的个数。实在是脑洞大开，一边是虚无缥缈的复数域函数，一边是一个一个地素数计数，这两个看似风马牛不相及的概念会有如此紧密的联系，实在是匪夷所思。

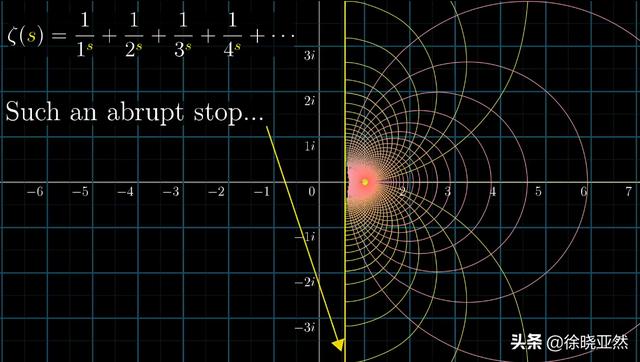
黎曼猜想非平凡零点的估计是数学界最大的谜题

黎曼猜想的内涵，我们这样的普通人是不可能体会到的，这里就简单介绍一下：

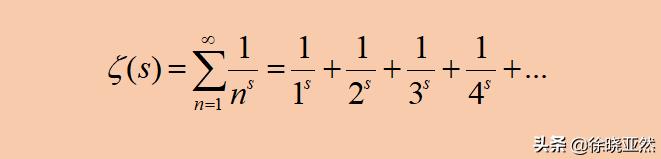
ζ级数

在整个复数域内有许多的s可以作为上述ζ函数的零点，其中一些负偶数就满足要求，因为这些负偶数都是显而易见的零点，我们就把这样的零点叫作平凡零点。既然有平凡零点，那么肯定就有非平凡零点，说的一点不错，有些看起来毫无规律的数也可以作为这个函数的零点。有人证明了这样的非平凡零点有无数个，黎曼猜想的内容就是所有满足条件的非平凡零点实部一定是1/2！

这个猜想的重要意义在哪儿呢？再来看看这个式子。

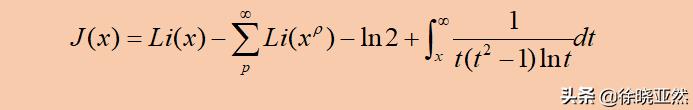
黎曼J（x）计数函数

这里的J(x)就是黎曼提出的素数计算公式。这里的J(x)不是粗糙的估计函数，而是准确值！由此得出，假若我们能够证明黎曼猜想，那么素数个数的问题就彻底解决！然而，黎曼猜想之所以被称为当今数学界最重要的问题，除了意义重大，还有就是非常艰深，远比我们熟悉的哥德巴赫猜想困难太多！

不过很可惜，到目前为止，人们关于黎曼猜想的最好结果是证明了，在x=1/2这条线上至少有40%的非平凡零点。一个从来不知道黎曼猜想的人恐怕也知道，这个成果和真正的黎曼猜想之间相隔千山万水！

素数公式周边的素数个数公式也这么难，看起来素数问题的确不是一个简单问题。先别着急，素数个数研究没有突出进展，那么素数分布呢？比如素数间隔。

那最著名的就是孪生素数猜想了。是否存在无穷多组相隔为2的素数对？

孪生素数猜想的先驱者——华人数学家张益唐

在很长一段时间聊，别说是否有无穷多对相隔为2的素数对这个问题难倒了世人，甚至，人们都不敢把存在无穷多对素数的间隔定义为有限多个长度。怎么理解呢？人们不知道是否存在无穷多组间隔在1亿，或者10亿的素数对。这里的1亿，10亿，100亿人们不能确定。只能去猜测可能是这样。直到有一位华人数学家第一次确定了这样的间隔是有限多的。

2013年，华人数学家张益唐证明了，存在无穷多组间隔在7000万以内的素数对。啊！人们终于放下心了，原来素数间隔真的是有限的!假若人们能够把这里的7000万缩小到2，那不就是证明了孪生素数猜想了么？事实证明，张益唐的方法不是一种孤立的独门秘籍，而是有着巨大的改造空间，在不到一年的时间里，人们就按照张益唐的方法将这个7000万缩小到了246，几乎就要成功了！

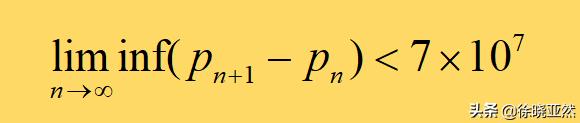
存在无穷多对间隔小于7000万的素数对

然而孪生素数跟我们开了玩笑，前面的进度飞快，越到后面，道路越难，甚至举步维艰。目前为止，数学界好像还没有确认过更好的成果，于是，孪生素数猜想仍然是一个不可遥望的梦。

我们再看看另外一个素数周边的问题，素数分拆问题呢？

陈景润

那不就是著名的哥德巴赫猜想么。中国人最熟悉不过的数学猜想了，到目前为止最好的结果是1+2，我国数学家陈景润先生在1973年得出的，快50年了，没有进展了。这个猜想的难度大家也绝对是深有体会，绝对不是表述的那么简单。老实说，晓然菌其实更加期待哥德巴赫猜想的解决，因为这个猜想上有太多中国人的情怀了。

素数个数，素数间隔，素数分拆，这三个素数领域的猜想，每个都是史诗级的问题，到目前为止，也没有一个问题能够被彻底解决。然而这三个难题的根源都是这个传说中的素数公式，由这个可能根本就不存在的素数通项公式就能引出这样巨大的难题.你还会以为这个公式可能会简单，甚至用初等方法就可以表示出来么？这是没有一丁点可能的！

素数分布螺旋

不过话也说回来，我们也许不用再对这个传说中的素数公式有期待了，可能根本就不存在这样的公式。呵呵，关于这样的公式是否存在，这好像又是一个巨大难题。真希望以后的数学界会出现伽罗瓦这样的天才，用他的理论明确告诉人们：请大家不要再对素数公式执迷不悟啦，我的理论证明了根本不存在这样的公式。

伽罗瓦——也许再等一百年就能预见下一个我了

即使真的没有这样的公式，也丝毫不妨碍数学家们继续在这份事业上开山劈地，为我们创造更多的成果。当数学成为所有人一种本能的时候，数学的春天才真的到来了。